7.Igualacion

IGUALACIÓN 

Resolver ecuaciones simultáneas, método de igualación

El sistema de ecuaciones simultáneas elegido es:

Es el primero de los métodos algebraicos  que estudiaremos y que se usan para resolver sistemas de ecuaciones simultáneas. En este caso, hablamos de dos ecuaciones  lineales con dos incógnitas.

¿Por qué se llama método de igualación?. Este método consiste en despejar la misma incógnita de las dos ecuaciones y posteriormente  igualar (de ahí su nombre) los segundos miembros de esos despejes, vale decir las dos expresiones algebraicas resultantes.

De este modo queda una ecuación de primer grado con una sola incógnita que debes resolver,  hallando la incógnita.  Sustituyendo ese valor en las dos ecuaciones originales y despejando la otra incógnita, resolverás el sistema inicial.

Te propongo un paso a paso bien claro y conciso.

1) Despejamos la misma incógnita de las dos ecuaciones. En este caso elegimos despejar la incógnita x, de ambas ecuaciones obteniendo los despejes siguientes:

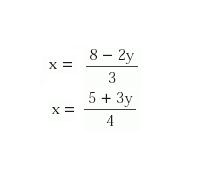
2) Igualamos los dos segundos miembros de ambas igualdades

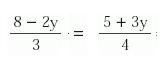
3) Resolvemos esta ecuación hasta hallar el valor de “y

32 -8 y = 15 + 9 y

-17 y = -32 + 15

– 17 y = -17

y= -17 / – 17

y = 1

4) Sustuimos el valor de “y” hallado en las dos ecuaciones simultáneas originales.

a)      3 x + 2 (1) = 8

b)     4 x – 3 (1) = 5

5) Resolvemos las ecuaciones, el valor de “x” que nos dé en ambos casos debería ser el mismo. Veamos los casos uno por uno:

a)            3x + 2 = 8

              3x = 8 – 2

              3x = 6

                 x = 6/3

                 x = 2”