UNIDAD EDUCATIVA
`` DIEZ DE AGOSTO ´´

INTEGRANTES: Paúl Chulde,Jhon Chuga,Elias Chanatasi


MATERIA: Proyecto


ASIGNATURA: Matematicas

LIC: WILLIAM TOBAR

Read More

20.SINPLIFICACION

 SINPLIFICACION

simplificar nos lleva al latín. En concreto, podemos establecer que se trata de un verbo que es fruto de la suma de dos componentes del latín: el adjetivo “simplex”, que puede traducirse como “simple”, y el verbo “facere”, que es sinónimo de “hacer”.

El concepto se vincula a lograr que algo se vuelva más simple: es decir, menos complejo, difícil o complicado. Por ejemplo: “No entiendo lo que quieres que haga: ¿podrías simplificar tus instrucciones?”, “Voy a simplificar mi idea: lo único que pretendo es que aprovechen mejor el tiempo de trabajo, no que pasen más horas en la oficina”, “El gobierno se comprometió a simplificar los trámites para la obtención de la licencia de conducir”.

El verbo simplificar, de este modo, puede emplearse en muchos ámbitos. Cuando la simplificación se vincula al lenguaje, hace referencia a cambiar el modo de explicación para que la comprensión de la información sea más sencilla. No es lo mismo decir “Voy a disputar un encuentro deportivo en el cual tendré que emplear mis pies para impulsar un balón y tratar de introducirlo en el arco rival” que “Voy a jugar al fútbol”. Mientras que la primera expresión es confusa, en la segunda se simplifica lo dicho.

Read More

19.SUMA DE POLINOMIOS

SUMA DE POLINOMIOS

Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.

P(x) = 2x³ + 5x − 3      Q(x) = 4x − 3x² + 2x³

1Ordenamos los polinomios, si no lo están.

Q(x) = 2x ³− 3x² + 4x

P(x) + Q(x) = (2x³ + 5x − 3) + (2x³ − 3x²+ 4x)

2Agrupamos los monomios del mismo grado.

P(x) + Q(x) = 2x³ + 2x³ − 3 x² + 5x + 4x − 3

3Sumamos los monomios semejantes.

P(x) + Q(x) = 2x³ + 2x³ − 3 x² + 5x + 4x − 3

También podemos sumar polinomios escribiendo uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.

P(x) = 7x⁴ + 4x² + 7x + 2      

Q(x) = 6x³ + 8x +3

P(x) + Q(x) =

= 7x⁴ + 6x³ + 4x² + 15x + 5

Read More

18.Trigonometría con la calculadora.

Trigonometría con la calculadora.

En primer lugar , se debe comprobar el modo de la unidad Angular en la que está funcionando la calculadora . Generalmente, la unidad por defecto es el grado Sexagesimal, de no ser así, es necesario consultar el manual Para aprender a utilizar el modo en radianes y el modo Sexagesimal. Para hallar el seno 25 grados y cos 95 grados con ayuda de la calculadora se produce como sigue . Para seno 25 grados se digita la secuencia Según el tipo de calculadora , puede variar el orden en el que se digita para obtener resultados se puede expresar en la calculadora científica por que en las otras no es posible sacar el seno, coseno, tangente.

Read More

17.Circunferencia goniometría

Circunferencia goniometría.

Las definiciones de seno, coseno y tangente se pueden Extender a un ángulo cualquiera haciendo uso de un sistema de coordenadas cartesianas y una circunferencia de centro 0 y radio 1 denominada circunferencia goniometría Cada ángulo x de un punto sobre un punto sobre La circunferencia goniometría el radio y las coordenadas de este punto forman un triangulo rectángulo . así para calcular los valores seno x t tan x para el ángulo x de la Figura 1 , se puede hacer el siguiente razonamiento . Como x pertenece al tercer cuadrante entonces seno x tiene la Igualdad de tan x se puede hacer en la calculadora sacar el seno el tan .

Read More

16.La recta real.

La recta real.

La recta real cumple con algunas características, tal Como se observa en la figura. -al punto de la referencia arbitrario llamado origen Le corresponde el número real llamado cero. -dada una unidad convierte en una medición, Cada numero positivo ‘m’ unidades de la Derecha del origen , y cada numero negativo –x se Representa mediante de un punto de una distancia De x unidades a la izquierda de el origen. Las flechas a la izquierda y a la derecha significa Que el conjunto de números reales en infinito Nunca tiene fin los números son infinitos .

Read More

15.Números irracionales en la recta.

Números irracionales en la recta.

Para ubicar algunos números irracionales en la recta Numérica se llevan a cavo los siguientes pasos. Se taza una recta e se ubican los números Sobre la posición del numero 1 se traza una línea Perpendicular con la misma longitud que la unidad Se une con un segmento el 0 y el segmento superior Perpendicular que se trazo anterior mente con un compas se ase centro en cero y se traza un arco desde la parte superior del segmento perpendicular asta cortar la recta numérica. Esto puede dar como resultado raíz de 2 O cualquier otro punto que se desee encontrar en el segmento numérico correspondiente.

Read More

14.MEDIDA DE LOS ANGULOS

MEDIDA DE LOS ANGULOS

Para hallar la medida de los ángulos centrales A y b se fija como primer ángulos el semieje Positivo de las obsesas Si el sentido de giro es contrario al de las agujas del reloj las medidas de los ángulos es un numero positivo si el sentido es el mismo de las manecillas es en número negativo. El grado sexagesimal es la medida de cada uno de sus ángulos que suman al dividir sus ángulos rectos en 90 partes iguales para expresar el ángulo de la suma de un numero entero y un ángulo menor se divide de modo que el cociente es el numero de vueltas y el residuo es el ángulo buscado como el ángulo de una sir conferencia abarca todo lo que abarca.

Read More

13. FUNCION CUADRATICA

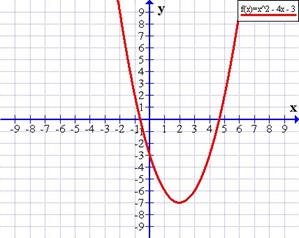
FUNCION CUADRATICA

En matemáticas, una función cuadrática de una variable es una función polinómica definida por:

${\displaystyle y=ax^{2}+bx+c\,}$

con ${\displaystyle a\neq 0}$.¹ También se da el caso que se le llame Trinomio cuadratico ² . También se denomina función cuadrática a funciones definidas por polinomios cuadráticos de más de una variable, por ejemplo:

${\displaystyle f(x,y)=Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F}$

En este caso el conjunto de puntos que resultan al igualar el polinomio a cero representan lugares geométricos que siempre es posible reducir a una de las formas:

${\displaystyle \left({\frac {x}{a}}\right)^{2}\pm \left({\frac {y}{b}}\right)^{2}=c^{2},\qquad \left({\frac {x}{a}}\right)^{2}\pm {\frac {y}{b}}=c}$

Que corresponden a tres tipos de sección (elipse, hipérbola y parábola).

Read More

12.SISTEMA DE INECUACION DE PRIMER GRADO

SISTEMA DE INECUACION DE PRIMER GRADO 

Si sumamos (o restamos) la misma cantidad en los dos miembros de una desigualdad, la desigualdad no varía. En el caso de una inecuación obtenemos una inecuación equivalente. Igual ocurre con el producto si multiplicamos (o dividimos) los dos miembros de una desigualdad por la misma cantidad positiva: la desigualdad no varía. Sin embargo, si multiplicamos (o dividimos) los dos miembros de una inecuación por una misma cantidad negativa, la desigualdad cambia de sentido. Así pues, cuando manipulemos inecuaciones y multipliquemos o dividamos ambos miembros por la misma cantidad obtendremos inecuaciones equivalentes, pero tendremos cuidado cuando lo hagamos con una cantidad negativa pues en ese caso la inecuación equivalente a la anterior tendrá cambiado el sentido de la desigualdad. Mejor lo vemos con un ejemplo.

Resolvamos la siguiente inecuación de primer grado:

2(x+1)3

−

3(2x−1)2

+x≤4−

3x+16

$$\frac{2(x+1)}{3}-\frac{3(2x-1)}{2}+x\le 4-\frac{3x+1}{6}$$

Se procede exactamente igual que en una ecuación de primer grado (eliminamos paréntesis y denominadores, trasponemos términos y reducimos términos semejantes). En este caso multiplicamos todos los términos (los dos miembros de la desigualdad) por 

6

$6$, que es el mínimo común múltiplo de los denominadores y luego procedemos a ir simplificando hasta obtener una desigualdad completamente reducida.Veámoslo:

Read More

11. RESOLUCIÓN DE SISTEMA POR EL MÉTODO GRAFICO

RESOLUCIÓN DE SISTEMA POR EL MÉTODO GRAFICO

Cada una de las ecuaciones que forman un sistema lineal de dos ecuaciones con dos incógnitas es la de una función de primer grado, es decir, una recta. El método gráfico para resolver este tipo de sistemas consiste, por tanto, en representar en unos ejes cartesianos, o sistema de coordenadas, ambas rectas y comprobar si se cortan y, si es así, dónde. Esta última afirmación contiene la filosofía del proceso de discusión de un sistema por el método gráfico. Hay que tener en cuenta, que, en el plano, dos rectas sólo pueden tener tres posiciones relativas (entre sí): se cortan en un punto, son paralelas o son coincidentes (la misma recta). Si las dos rectas se cortan en un punto, las coordenadas de éste son el par (x, y) que conforman la única solución del sistema, ya que son los únicos valores de ambas incógnitas que satisfacen las dos ecuaciones del sistema, por lo tanto, el mismo es compatible determinado

1. Se despeja la incógnita y en ambas ecuaciones.
2. Se construye, para cada una de las dos funciones de primer grado obtenidas, la tabla de valores correspondientes.
3. Se representan gráficamente ambas rectas en los ejes coordenados.
4. En este último paso hay tres posibilidades:
   1. Si ambas rectas se cortan, las coordenadas del punto de corte son los únicos valores de las incógnitas x e y. Sistema compatible determinado.
   2. Si ambas rectas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa recta en la que coinciden ambas. Sistema compatible indeterminado.
   3. Si ambas rectas son paralelas, el sistema no tiene solución. Sistema incompatible.

Read More

10. REGLAS DE CRAMER

REGLAS DE CRAMER

Para la resolución de un sistema de dos ecuaciones con dos incógnitas, de la forma. Dado el sistema de ecuaciones:

${\displaystyle a{\color {blue}x}+b{\color {blue}y}={\color {red}e}\,}$

${\displaystyle c{\color {blue}x}+d{\color {blue}y}={\color {red}f}\,}$

Se representa matricialmente :

${\displaystyle {\begin{bmatrix}a&b\\c&d\end{bmatrix}}{\begin{bmatrix}{\color {blue}x}\\{\color {blue}y}\end{bmatrix}}={\begin{bmatrix}{\color {red}e}\\{\color {red}f}\end{bmatrix}}}$

Entonces, ${\displaystyle x}$ e ${\displaystyle y}$ pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:

${\displaystyle x={\frac {\begin{vmatrix}\color {red}{e}&b\\\color {red}{f}&d\end{vmatrix}}{\begin{vmatrix}a&b\\c&d\end{vmatrix}}}={\frac {{\color {red}e}d-b{\color {red}f}}{ad-bc}};\quad y={\frac {\begin{vmatrix}a&\color {red}{e}\\c&\color {red}{f}\end{vmatrix}}{\begin{vmatrix}a&b\\c&d\end{vmatrix}}}={\frac {a{\color {red}f}-{\color {red}e}c}{ad-bc}}}$

Ejemplo[editar]

Ejemplo de la resolución de un sistema de 2x2:

Dado

${\displaystyle 3x+1y=9\,}$

${\displaystyle 2x+3y=13\,}$

que matricialmente es:

${\displaystyle {\begin{bmatrix}3&1\\2&3\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}9\\13\end{bmatrix}}}$

x e y pueden ser resueltos usando la regla de Cramer

${\displaystyle x={\frac {\begin{vmatrix}9&1\\13&3\end{vmatrix}}{\begin{vmatrix}3&1\\2&3\end{vmatrix}}}={9\cdot 3-1\cdot 13 \over 3\cdot 3-1\cdot 2}=2}$

${\displaystyle y={\frac {\begin{vmatrix}3&9\\2&13\end{vmatrix}}{\begin{vmatrix}3&1\\2&3\end{vmatrix}}}={3\cdot 13-9\cdot 2 \over 3\cdot 3-1\cdot 2}=3}$

Read More

9.METODO DE GAUSS

MÉTODO DE GAUSS

Es un método iterativo, lo que significa que se parte de una aproximación inicial y se repite el proceso hasta llegar a una solución con un margen de error tan pequeño como se quiera. Buscamos la solución a un sistema de ecuaciones lineales, en notación matricial:

donde:

${\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nn}\end{bmatrix}},\qquad x={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}},\qquad b={\begin{bmatrix}b_{1}\\b_{2}\\\vdots \\b_{n}\end{bmatrix}}.}$

El método de iteración Gauss-Seidel se computa, para la iteración ${\displaystyle (k+1)\,}$:

${\displaystyle x^{(k+1)}=Mx^{(k)}+c.\,}$

donde

${\displaystyle A=N-P\,}$

definimos

${\displaystyle M=N^{-1}P\,}$

y

${\displaystyle c=N^{-1}b\,}$,

donde los coeficientes de la matriz N se definen como ${\displaystyle n_{ij}=a_{ij}\,}$ si ${\displaystyle i{\leq }j}$, ${\displaystyle n_{ij}=0\,}$ si ${\displaystyle i>j\,}$.

Considerando el sistema ${\displaystyle Ax=b,\,}$ con la condición de que ${\displaystyle a_{ii}{\neq }0,i=1,...,n\,}$. Entonces podemos escribir la fórmula de iteración del método

${\displaystyle x_{i}^{(k+1)}={\frac {-\sum _{1{\leq }j{\leq }i-1}a_{ij}x_{j}^{(k+1)}-\sum _{i+1{\leq }j{\leq }n}a_{ij}x_{j}^{(k)}+b_{i}}{a_{ii}}},i=1,...,n\,}$(*)

La diferencia entre este método y el de Jacobi es que, en este último, las mejoras a las aproximaciones no se utilizan hasta completar las iteraciones.

Read More

8.Reduccion

REDUCCIÓN

1. Se preparan las dos ecuaciones, multiplicándolas por los números que convenga.

2. La restamos, y desaparece una de las incógnitas.

3. Se resuelve la ecuación resultante.

4. El valor obtenido se sustituye en una de las ecuaciones iniciales y se resuelve.

5. Los dos valores obtenidos constituyen la solución del sistema.

Te propongo aprender hoy el tercero de los métodos de resolución de un sistema de ecuaciones, esto es el método de reducción.  Si quieres repasar o practicar los que vimos anteriormente, aquí mismo te dejo vínculo al primero de los métodos algebraicos que vimos, el  método de igualación y al segundo, esto es, el método de sustitución

Este nuevo método para resolver un sistema de ecuaciones simultáneas, recibe el nombre de método de reducción, porque precisamente eso trataremos de hacer con las incógnitas comunes en ambas ecuaciones.

Read More

7.Igualacion

IGUALACIÓN 

Resolver ecuaciones simultáneas, método de igualación

El sistema de ecuaciones simultáneas elegido es:

Es el primero de los métodos algebraicos  que estudiaremos y que se usan para resolver sistemas de ecuaciones simultáneas. En este caso, hablamos de dos ecuaciones  lineales con dos incógnitas.

¿Por qué se llama método de igualación?. Este método consiste en despejar la misma incógnita de las dos ecuaciones y posteriormente  igualar (de ahí su nombre) los segundos miembros de esos despejes, vale decir las dos expresiones algebraicas resultantes.

De este modo queda una ecuación de primer grado con una sola incógnita que debes resolver,  hallando la incógnita.  Sustituyendo ese valor en las dos ecuaciones originales y despejando la otra incógnita, resolverás el sistema inicial.

Te propongo un paso a paso bien claro y conciso.

1) Despejamos la misma incógnita de las dos ecuaciones. En este caso elegimos despejar la incógnita x, de ambas ecuaciones obteniendo los despejes siguientes:

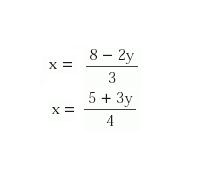
2) Igualamos los dos segundos miembros de ambas igualdades

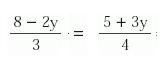
3) Resolvemos esta ecuación hasta hallar el valor de “y

32 -8 y = 15 + 9 y

-17 y = -32 + 15

– 17 y = -17

y= -17 / – 17

y = 1

4) Sustuimos el valor de “y” hallado en las dos ecuaciones simultáneas originales.

a)      3 x + 2 (1) = 8

b)     4 x – 3 (1) = 5

5) Resolvemos las ecuaciones, el valor de “x” que nos dé en ambos casos debería ser el mismo. Veamos los casos uno por uno:

a)            3x + 2 = 8

              3x = 8 – 2

              3x = 6

                 x = 6/3

                 x = 2”

Read More